The Famous Probability Question for the Admission of Mathematics Department of Moscow University (Probability Problem)
- Emir Polat

- 6 Mar 2022
- 3 dakikada okunur
Moscow State University, ranked among the top 100 most qualified universities in the world, selects its staff and students with great care and subjects them to demanding admission process. In recent years, a probability question asked at the stage of admission to the mathematics department of this university has attracted the attention of many people and aroused their curiosity. In this article, I will explain and examine this mathematical question and its solution. In this probability problem, two people agree to meet at a certain place. Both of them arrive at this place at any time between 12:00 and 13:00. After waiting at that location for 15 minutes, they leave. If they meet within these 15 minutes, their meeting will take place, otherwise they will not meet. So, with what percentage probability will these two people meet?
Since the one mentioned here is not a finite set, I will examine the solution of the problem using the graphical method.
Let these two individuals be "x" and "y". Since the time interval we are examining is 1 hour, we can examine this time interval in minutes. Since both individuals will be in this place in this particular 60 minutes, we can start the solution by drawing the graph below:
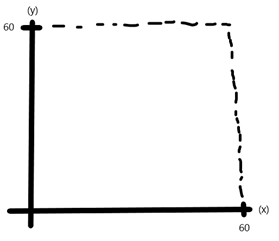
If there is a difference of more than 15 units between the numbers in x and y pairs expressed by the points marked on this graph, these two people cannot meet. Let's formulate this as an inequality:
“y ≤ x + 15” (person y must arrive before or at the same time as the 15-minute segment in which person x arrives)
It is also "x ≤ y + 15". (The same is true for person x.)
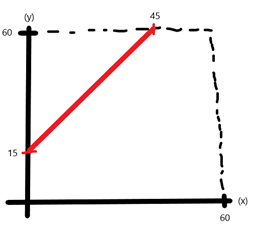
If we apply the first inequality to the coordinate plane, we get a straight line like this. Accordingly, if we apply this inequality to a random point to find the area we need to scan:
When we try the point (20,20), we come across the inequality of 20 ≤ 35, and as can be seen, this ordered pair provides this inequality. So at this stage we can scan the lower part of the line.
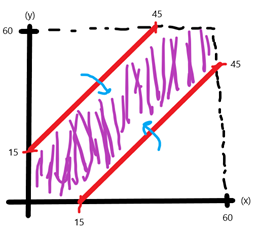
If we add the second inequality to the coordinate plane and check again by applying any point to the inequality, we see that the upper part of this line should be scanned.
As a result, we reach that the values between the two lines (in the shaded area) provide the equality. That is, if two individuals arrive at the times in ordered pairs in this range, they can meet up.
Now, we can move on to the probability calculation:
First we find the whole coordinate plane area: 60. 60 = 3600
Next, we find the area of the triangles outside the shaded area: The sum of the areas outside the shaded area is 452 from 2. (45. 45/2 + 45.45/2).
To find the desired area (shaded area), we subtract the area outside the shaded portion from the whole area: 602 – 452 = (60 – 45). (60 + 45) = 15. 105 = 1575
When we compare the whole area with the desired area, we get 1575 / 3600 = 7/16. When we divide 7 by 16, the result is approximately 43/100.
That is, if these two individuals arrive at this location at any time during this hour and wait there for 15 minutes, the probability that they will meet is approximately 43%.
In my opinion, this is a surprisingly high rate, because it is quite interesting and remarkable that two people who do not know each other's arrival time in a large time interval meet at a rate of almost 50%, that is, approximately in one of two possible ways, without any communication.


